使用scikit-learn和Keras建立房价估价模型
之前曾写过一篇抓取 搜房网 (fang.com) 房源数据并用 tflean 搭建神经网络进行房价分类的文章。
本文算是上面这篇文章的第二个版本:使用 scikit-learn 和 Keras 来对广州二手房房源数据搭建 回归模型 进行房源价格的估价。
数据抓取
相比于第一次抓取时,搜房网对房源页面进行了改版,因此之前所使用的抓取脚本不能使用了。于是又用 beautifulsoup 改了一遍,解析取出每一项信息然后结构化。
然后再对各项非数字内容进行数字映射,如:
regions = {'天河': '1.0', '荔湾': '2.0', '海珠': '3.0', '越秀': '4.0', '白云': '5.0', '番禺': '6.0', '黄埔': '7.0', '增城': '8.0', '花都': '9.0', '从化': '10.0', '南沙': '11.0'}
最终的部分结果如下:
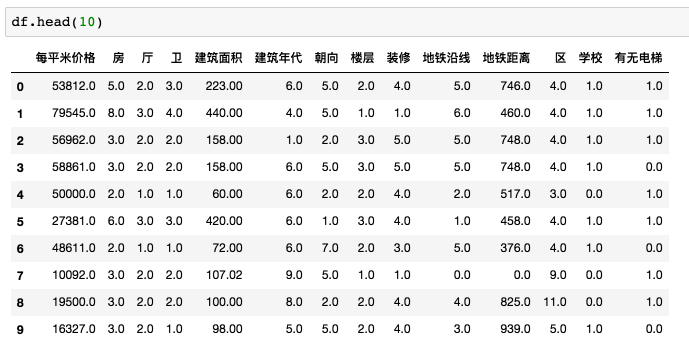
需要说明的是,我排除了每平米价格在 20万 以上的房源 ( 只有 3 例 ),土豪的世界我并不关心。
跟上一次抓取数据时相比,搜房网目前还能抓到房源是否在哪条地铁线路附近、距离地铁多远。

常识告诉我们,这也是影响房价的一个重要因素,因此也作为了特征值。
数据总行数为 10309 :
In [4]: df.shape[0]
Out[4]: 10309
先看下两个图了解下房价数据:
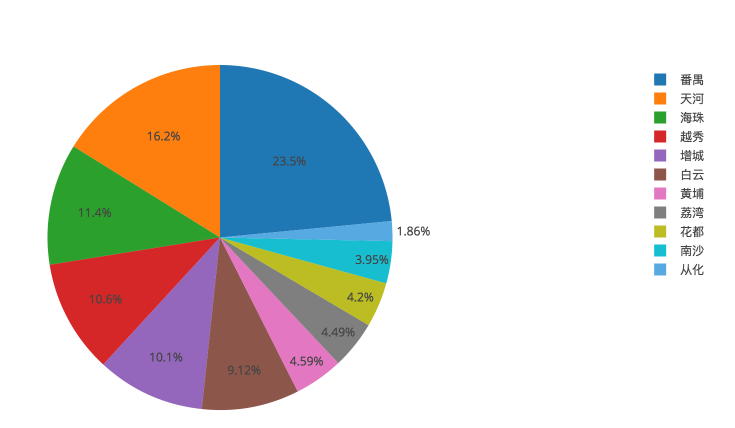
( 广州各区房源比例 )
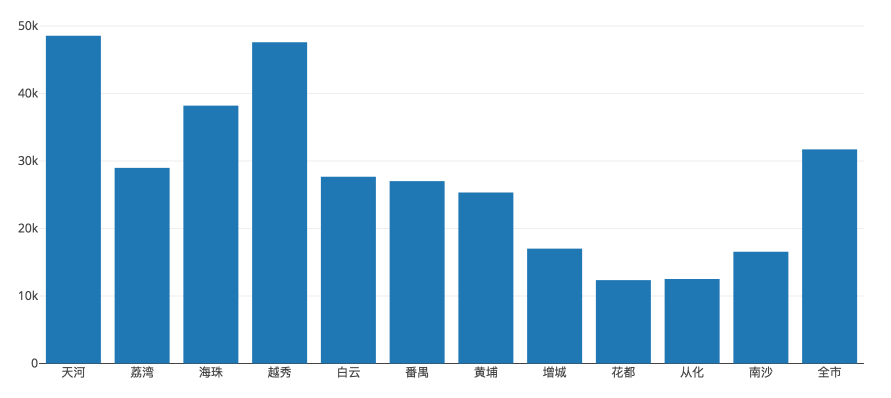
( 广州各区平均房价,最后一列为全市均价 )
具体均价如下:
{
'天河': 48545.516516516516,
'荔湾': 28983.626349892009,
'海珠': 38201.262574595057,
'越秀': 47588.640838650863,
'白云': 27656.089361702128,
'番禺': 27007.389256198348,
'黄埔': 25335.879492600423,
'增城': 17014.85277246654,
'花都': 12356.367205542725,
'从化': 12507.666666666666,
'南沙': 16559.167076167076,
'全市': 31709.176156756232
}
上一次抓数据的时候(四月份),全市均价还是 28995.8 ,三个月内广州的房价又上涨了 2713.4 元每平米。
备注:数据收集日期:2017/07/23 - 2017/07/25
导入数据并分为训练数据和测试数据
from pandas import read_csv
df = read_csv('./dataset.csv')
train_ = df[0:df.shape[0]-1000]
test_ = df[df.shape[0]-1000:]
predictors = ['房','厅','卫','建筑面积','建筑年代','朝向','楼层','装修','地铁沿线','地铁距离','区','学校','有无电梯']
X_train = train_[predictors]
y_train = train_['每平米价格']
X_test = test_[predictors]
y_test = test_['每平米价格']
将最后 1000 条数据作为验证模型正确率而使用的测试数据,其余数据为训练数据。
选择 SVR 模型
使用 scikit-learn 的 SVR() 模型,使用默认的核函数 rbf
class sklearn.svm.SVR(kernel='rbf', degree=3, gamma='auto', coef0=0.0, tol=0.001, C=1.0, epsilon=0.1, shrinking=True, cache_size=200, verbose=False, max_iter=-1)
gamma 默认值为 1/n,其中 n 为特征值的数量,我们的例子中 n = 13,折中取了 0.1。
另外一个比较重要的参数是 C (惩罚因子,即对误差的宽容度。C 越高,说明越不能容忍出现误差,容易过拟合。C 越小,容易欠拟合)。
具体原理可以参考这篇文章
先简单测试下 C 参数:
from sklearn.svm import SVR
for i in range(0, 7):
C = 10**i
clf = SVR(kernel='rbf', C=C, gamma=0.1)
clf.fit(X_train, y_train)
print "C=%d, score=%f" % (C, clf.score(X_train, y_train))
输出如下:
C=1, score=-0.031758
C=10, score=-0.020476
C=100, score=0.061383
C=1000, score=0.295201
C=10000, score=0.765092
C=100000, score=0.995138
C=1000000, score=0.999077
结果也验证了 C 越大,对于训练集的数据的准确度越高,先选择 C=1000000,至于是否会过拟合,我们等下再用测试集数据来验证下情况。
训练结果
import matplotlib.pyplot as plt
clf = SVR(kernel='rbf', C=1000000, gamma=0.1)
clf.fit(X_train, y_train)
print clf.score(X_train, y_train)
predict = clf.predict(X_train)
plt.scatter(predict, y_train, s=2)
predict_y = clf.predict(X_train.values[4])
print "predict: %.2f, actually: %.2f" % (predict_y, y_train.values[4])
plt.plot(predict_y, predict_y, 'ro')
plt.plot([y_train.min(), y_train.max()], [y_train.min(), y_train.max()], 'k--', lw=2)
输出结果:
0.999076822472
predict: 49999.90, actually: 50000.00
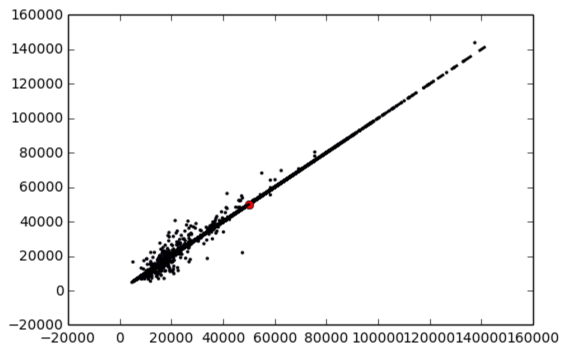
斜线为真实值线,黑点为预测值,从图上可以看到这个模型在训练集上的预测值和真实值基本吻合了。
使用测试数据验证模型准确度
predict_test = clf.predict(X_test)
print clf.score(X_test, y_test)
plt.scatter(predict_test, y_test, s=2)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=2)
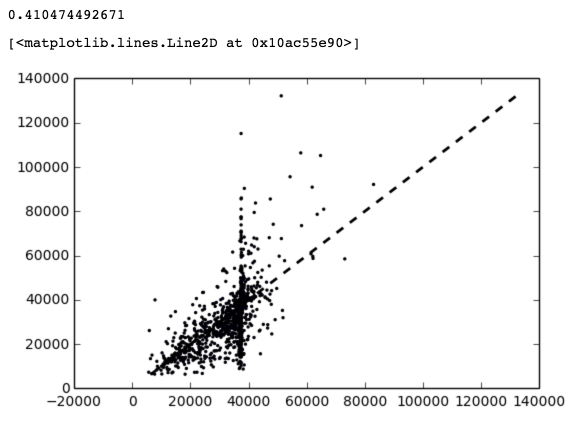
可以看到数据比较明显地分为了两拨,一拨是比较拟合真实值的斜线,另外一拨是在 x=40000 附近的垂直线。( 不明白为什么会出现这种集中在某个预测值的情况 )
准确率只有 41% ,再用 sklearn 的交叉验证函数跑 10 遍:
from sklearn.model_selection import cross_val_score
y = df['每平米价格']
X = df[predictors]
scores = cross_val_score(clf, X, y, cv=10)
print scores
print scores.mean()
cross_val_score 函数会自动将全部数据分为 10 份,然后将其中 9 份数据作为训练集,剩下的一份作为测试集,然后会跑 10 次交叉验证。
( 跑了好久 ... )
输出结果:
[ 0.37906349 0.3947758 0.5191052 0.44455579 0.45646649 0.39464724
0.4439831 0.4434501 0.41471762 0.39988068]
0.429064549048
可以看到平均下来的准确度也就 42.9% 。
优化模型
改下惩罚因子试下是否有改善:
clf = SVR(kernel='rbf', C=50000, gamma=0.1)
clf.fit(X_train, y_train)
print clf.score(X_train, y_train)
scores = cross_val_score(clf, X, y, cv=10)
print scores
print scores.mean()
( 又跑了好久 ... )
结果:
0.985096477399
[ 0.37902499 0.40034578 0.52363507 0.44748625 0.44871473 0.39534226
0.43854683 0.4470296 0.41939679 0.40100924]
0.43005315467
嗯,提高了 0.1%。
做下 Grid Search,意思是给出备选参数值,让它自动跑出一个最佳的参数值:
from sklearn.model_selection import GridSearchCV
parameters = {'C': range(30000, 100000, 10000)}
svr = SVR(kernel='rbf', gamma=0.1)
clf = GridSearchCV(svr, parameters, cv=10)
clf.fit(X, y)
print clf.best_params_
( 又跑了好久 ... )
结果:
{'C': 70000}
用 C=70000 重新跑了一次交叉验证:
结果:
[ 0.38117769 0.39773934 0.52183782 0.44646927 0.45482664 0.39650662
0.44513795 0.44663406 0.41807075 0.4017944 ]
0.431019453481
又提高了 0.1% ...
看下 scikit-learn 的文档,其中有提到 数据预处理 方面的问题:

个人理解,不太准确,大概的意思是将每个特征值按一定的规则缩放到一个比较小的范围。好比说从 1 到 100,误差可能会较大,但是缩放到从 0 到 1 的范围,误差就相对较小。
预处理之后的模型情况如下:
from sklearn import preprocessing
X = preprocessing.scale(X_train)
y = y_train
clf = SVR(kernel='rbf', C=40000, gamma=0.1)
clf.fit(X, y)
print "training score: %f" % clf.score(X, y)
X_test = preprocessing.scale(X_test)
predict_test = clf.predict(X_test)
print "testing score: %f" % clf.score(X_test, y_test)
( 需要注意的是,必须对训练数据和测试数据都进行 scale 操作;之前已做了 Grid Search,scale 之后的训练数据,最佳的 C 参数为 40000 )
结果:
training score: 0.712182291727
testing score: 0.575817605735
可以看到虽然训练集的表现不甚理想,但是测试集的准确度比之前上升了 13% ,达到了 57.6%,看起来效果还是不错的。
对数据做了 scale 之后有一个问题,比如说我有一个新的数据需要预测,这时候我根本不知道应该怎么缩放以适应训练好的模型,所以需要记录下缩放的规则,然后用规则对新数据做同样的 scale 变换,才能进行预测:
scaler = preprocessing.StandardScaler().fit(X_train)
new_data = [3.0,2.0,1.0,84.0,8.0,6.0,2.0,4.0,3.0,200.0,1.0,1.0,1.0]
new_data = scaler.transform(new_data)
print clf.predict(new_data)
接下来,我们再用所有数据做下交叉验证,看下准确率:
y = df['每平米价格']
X = preprocessing.scale(df[predictors])
scores = cross_val_score(clf, X, y, cv=10)
print scores
print scores.mean()
结果:
[ 0.55006725 0.54573057 0.61465035 0.52750594 0.59165464 0.57390134
0.6096038 0.55271578 0.50174115 0.57151666]
0.563908747408
预测值如下,可以看到不像之前那样分为两拨了:
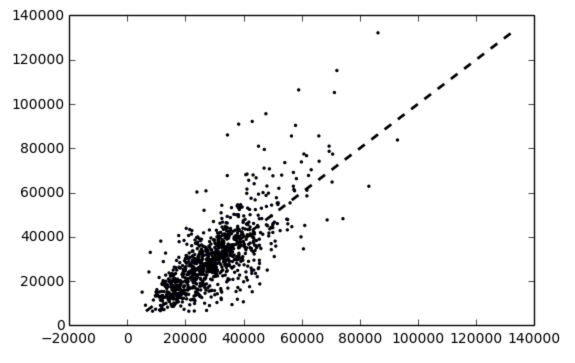
之后再做了 C 和 gamma 两两组合的 Grid Search,并没有得到比较明显的提升。
Give me more data!
再次收集了近 3000 条数据 (共 12937 条数据),再次按照之前的步骤进行参数选择,重新执行交叉验证,可以看到准确度进一步提升了 2%:
[ 0.58394156 0.57893039 0.61247822 0.54683733 0.59447176 0.62030941
0.6107769 0.5726037 0.56656728 0.55000072]
0.583691726816
嗯,考试前多做点习题还是很有用的。
特征选择
特征选择本来应该在训练模型之前进行。特征选择的作用在于分析出影响最大的几个特征值,排除一些次要的特征值,可以提高训练的速度,但是对于准确度来说,可能会提高也可能会降低,说不定。
不过我们在这里做下特征选择,看下影响房价的最重要的五个因素是什么:
from sklearn.feature_selection import RFE
model = SVR(kernel='linear')
rfe = RFE(model, 5)
rfe = rfe.fit(X.values, y.values)
for i, v in enumerate(rfe.support_):
if v:
print predictors[i]
结果如下:
房
卫
地铁沿线
区
学校
( 说明下,上面的五个特征值的重要性并不是排序的 )
上面说明了这么个结论:在哪个区、是否在地铁附近、有无学位、房间数和卫生间数 是影响房价的最重要的五个因素。
貌似也符合常识。
模型的保存和导入
训练好的模型应当保存下来,方便导入。
from sklearn.externals import joblib
joblib.dump(clf, './model.pkl')
导入:
clf = joblib.load('./model.pkl')
深度学习
接下来尝试用深度学习做回归。
这里使用 Keras 的 scikit-learn 接口包装器 ( keras.wrappers.scikit_learn.KerasRegressor ) 来进行房价的回归估值。
需要导入的模块:
from pandas import read_csv
import numpy
from keras.models import Sequential
from keras.layers import Dense
from keras.wrappers.scikit_learn import KerasRegressor
from sklearn import preprocessing
from sklearn.pipeline import Pipeline
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.cross_validation import cross_val_predict
import matplotlib.pyplot as plt
导入数据、划分训练集和测试集,与之前用 scikit-learn 一样:
train_ = df[0:df.shape[0]-1000]
test_ = df[df.shape[0]-1000:]
predictors = ['房','厅','卫','建筑面积','建筑年代','朝向','楼层','装修','地铁沿线','地铁距离','区','学校','有无电梯']
y_train = train_['每平米价格']
X_train = train_[predictors]
X_test = test_[predictors]
y_test = test_['每平米价格']
scale 预处理:
X = preprocessing.scale(X_train)
y = preprocessing.scale(y_train)
x_scaler = preprocessing.StandardScaler().fit(X_train)
y_scaler = preprocessing.StandardScaler().fit(y_train)
( 在使用 SVR 时,我没有做 y 的 scale 操作,因为发现把 y 数据 scale 之后,模型训练了一晚上都没有出结果,不知道是什么原因。)
建立模型:
def nn_model():
model = Sequential()
model.add(Dense(13, input_dim=13, kernel_initializer='normal', activation='relu'))
model.add(Dense(6, kernel_initializer='normal', activation='linear'))
model.add(Dense(1, kernel_initializer='normal'))
model.compile(loss='mae', optimizer='rmsprop')
return model
Dense 是全连接层,第一层全连接层,我们的数据有 13 个特征值,所以 input_dim 参数为 13。
activation 为激励函数,第一层这里选择了 relu。
然后再加一层全连接层作为隐藏层,激励函数选择 linear,参考这个链接:链接1
损失函数只能选择 mse 或者 mae,我这里用了 mae。
优化器用 rmsprop,当然也可以用 adam 之类的。
接下来使用 KFold 来做交叉验证,参考这个链接:链接2
seed = 7
numpy.random.seed(seed)
estimators = []
estimators.append(('mlp', KerasRegressor(build_fn=nn_model, epochs=200, batch_size=32, verbose=0)))
pipeline = Pipeline(estimators)
kfold = KFold(n_splits=5, random_state=seed)
开始交叉验证:
scores = cross_val_score(pipeline, X, y, cv=kfold)
print scores
print scores.mean()
plt.scatter(predicted, y, s=2)
plt.plot(y, y, 'ro', lw=2)
结果如下:
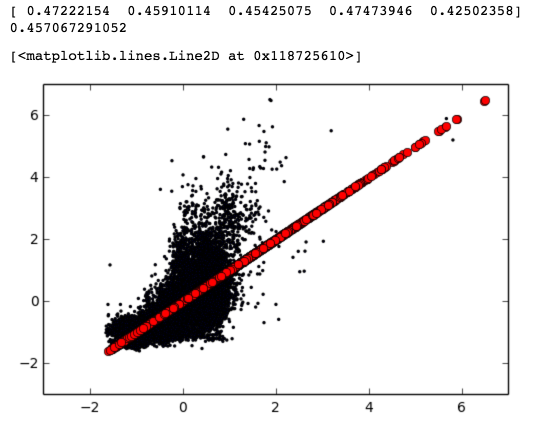
需要注意的是,这里的 score 并不像用 scikit-learn 的 SVR 时的准确率,而是 loss 函数的数值,即 mae ( Mean Absolute Error ),因为 accuracy 是不能参考的。参考链接1:
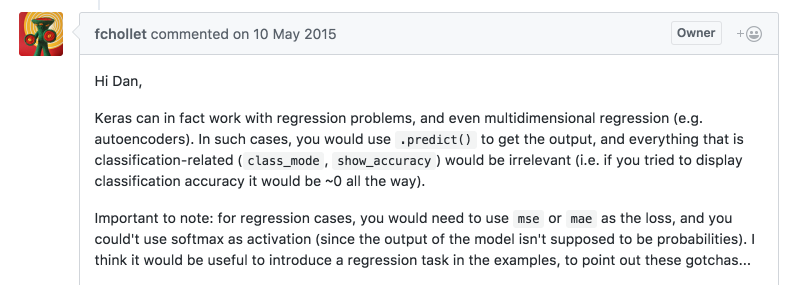
从打印的预测值点图来看,比较发散,并不算理想。
我们尝试改进一下模型,加多一层隐藏层:
def nn_model():
model = Sequential()
model.add(Dense(13, input_dim=13, kernel_initializer='normal', activation='relu'))
model.add(Dense(6, kernel_initializer='normal', activation='relu'))
model.add(Dense(3, kernel_initializer='normal', activation='linear'))
model.add(Dense(1, kernel_initializer='normal'))
model.compile(loss='mae', optimizer='rmsprop')
return model
然后将训练轮次增加到 500:
estimators.append(('mlp', KerasRegressor(build_fn=nn_model, epochs=500, batch_size=32, verbose=0)))
结果:
[ 0.42803601 0.39274284 0.41864015 0.40990664 0.38228733]
0.406322592681
可以看到 mae 减少了 11%,意味着模型的预测值更加准确了,而预测值点图也说明了这点:
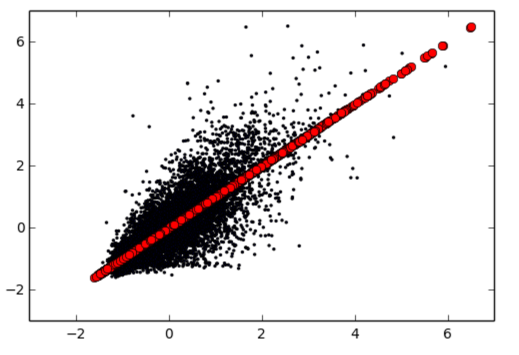
用一个自制的检查准确度的函数来看下,假设预测值与实际值误差不超过 10% 为准确的话:
import math
X_test = test_[predictors]
y_test = test_['每平米价格']
total = len(y_test)
cnt = 0
X_test = preprocessing.scale(X_test)
predicted = model.predict(X_test)
for i,v in enumerate(predicted):
p = y_scaler.inverse_transform(v)
r = y_test.values[i]
if math.fabs(r - p)/r < 0.1:
cnt += 1
print "accuracy: %d/%d" % (cnt, total)
输出:
accuracy: 268/1000
额,不到三成 ...
还有一种优化方案,就是链接2中的 Wider Network Topology,加大第一层的神经元数:
def nn_model():
model = Sequential()
model.add(Dense(20, input_dim=13, kernel_initializer='normal', activation='relu'))
model.add(Dense(10, kernel_initializer='normal', activation='relu'))
model.add(Dense(5, kernel_initializer='normal', activation='linear'))
model.add(Dense(1, kernel_initializer='normal'))
model.compile(loss='mae', optimizer='rmsprop')
return model
从结果来看确实有所提高准确度:
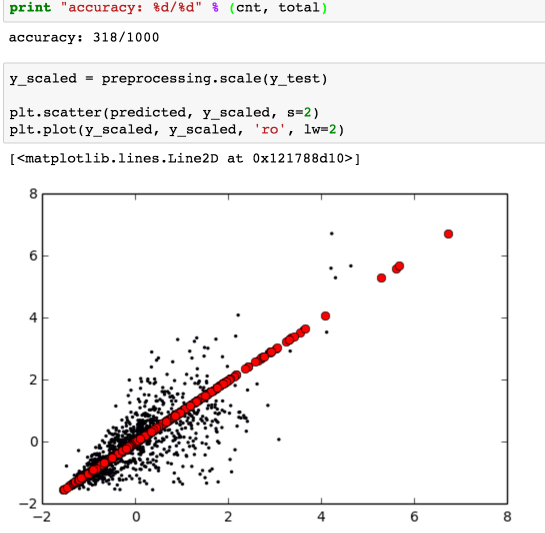
最后我们捏造两个数值来比较下 Keras 和 SVR 两种模型:
下面两组数据,一个是在天河区靠近地铁三号线 200 米左右有学位的房子;一个是在花都区没挨着地铁没学位的房子,两组数据其他都一样:
房,厅,卫,建筑面积,建筑年代,朝向,楼层,装修,地铁沿线,地铁距离,区,学校,有无电梯
3.0,2.0,2.0,133.0,7.0,2.0,2.0,4.0,3.0,200.0,1.0,1.0,1.0
3.0,2.0,2.0,133.0,7.0,2.0,2.0,4.0,0.0,0.0,9.0,1.0,1.0
结果:
| 房源 | Keras | SVR |
| 天河 | 80271.16 | 69902.54 |
| 花都 | 11703.23 | 14411.85 |
都正确地预估出天河的房子要比花都的要贵好多。
就这两组数据来说,个人感觉 Keras 比 SVR 更符合现实 ...
搭个页面应用
最后我们用 Flask 搭个简单的单页应用来做个房源估价应用。
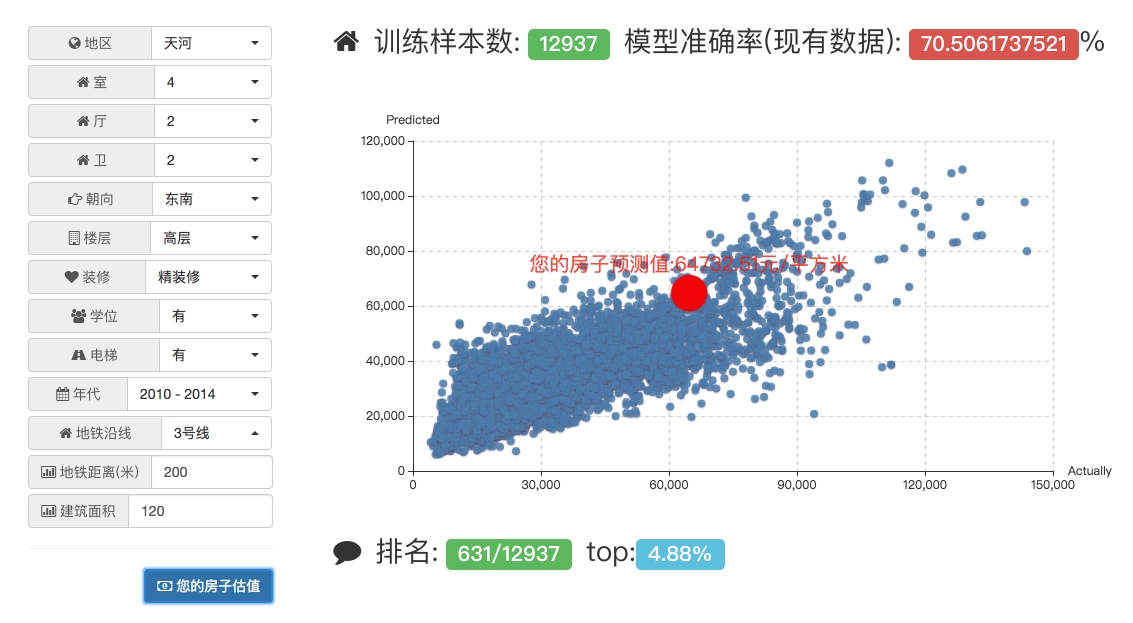
使用的是之前训练出来的 SVR 模型。
结论
- 得益于各种开源项目,目前上手机器学习和深度学习,门槛降低了很多;
- 房价还在疯狂上涨,我去 ...